In Example 9.4.6 of the textbook we return to our calculations from Example 3.5.13 but with our new perspectives from the Implicit Function Theorem and multivariable calculus in mind. This example analyzes an equation for the fraction A of a population that is ultimately infected during a disease outbreak.
As an example, Figure 1 plots data from a plague outbreak in Bombay India (now Mumbai) in 1905 showing estimates of the number of infected people over time (the data can be downloaded from the link at the left). Once the outbreak was over (at week 30, which was July 21, 1906) a certain fraction of the population had been infected. This is the quantity A from Example 9.4.6.
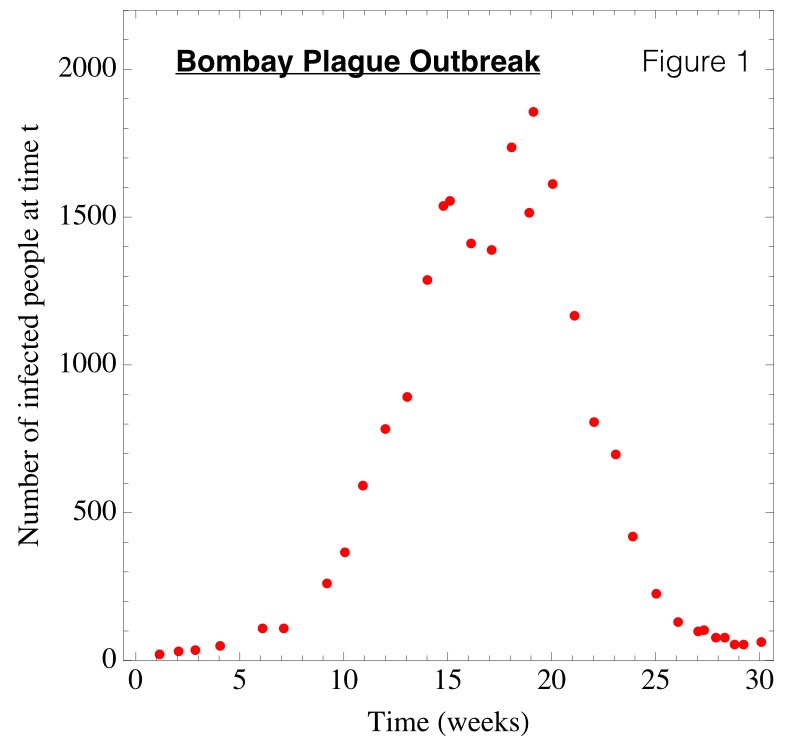
The data in Figure 1 were some of the first to be analyzed using mathematical models (see Kermack and McKendrick 1927). We explored such models in detail in other chapters of the textbook (for example, see Exercise 7.6.23 and the Project on page 354). The following animation allows you to explore the predicted outbreak for different choices of the constant q (we have set rho=1 from Example 9.4.6 in this animation). The red curve is the number of people infected at time t (analogous to the data in Figure 1). The blue curve is the number of people who have not yet been infected, again at time t. The blue curve starts at 10,000 (the total initial population size) when t = 0 and declines to some final value that depends on q. The quantity A is the total number of people that were infected during the outbreak divided by the total initial population size.
The above animation illustrates how the value of A changes when q is changed. Thus A is a function of q. In Example 9.4.6 of the textbook we calculated the derivative dA/dq, which gives the rate of change of A with respect to an increase in q. We can gain a better sense of what this derivative means epidemiologically as follows.
Suppose q = 2. From the above animation you can find that the fraction of the population ultimately infected is then A = 0.797. Now suppose q is increased a small amount to q = 2.1. Again you can use the above animation to find that A = 0.822 in this case. The derivative of A with respect to q can then be approximated as the increase in A per unit increase in q. This is calculated as
The derivative dA/dq is therefore approximately 0.25, meaning that the fraction of the population infected increases by approximately 0.25 for a unit increase in q.
To see how this ties together with the result from Example 9.4.6 of the textbook, let’s now also calculate the derivative from the expression obtained there. With rho=1 we obtain
The benefit of the result in Example 9.4.6 is that it is exact, and we can also obtain values of this derivative for any values of the constants very easily by simply substituting the relevant quantities.
References
Kermack, W.O. and A.G. McKendrick. 1927. A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London, Series A 115:700-721